Diagramme de Bode
L’expression d’un gain complexe n’est pas évidente pour étudier le comportement en fréquence d’un circuit électrique. Les diagrammes de Bode permettent rapidement de déduire de l’expression d’un gain complexe sont comportement en fréquence. Considérons l’exemple précédent :

- le module du gain est :

En décibel (db), ce gain devient :

Si w tend vers 0, le gain en db tend vers 0db, si w tend vers l’infini, le gain en db tend vers :
![]()
à savoir une droite en échelle logarithmique dont la pente est de –20db/décade. En conséquence, du point de vue asymptotique, le gain en db se décompose en deux droites. Le point de jonction de ces deux droites se nomme fréquence de coupure ou fréquence de cassure. Ce point est obtenu pour w égale à w0. A ce point, le gain en db vaut –3db. Le diagramme en amplitude est donc :
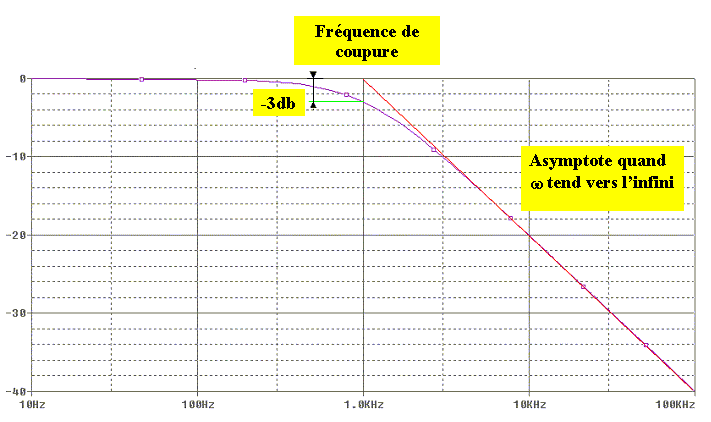
Il se confond quasiment avec ses asymptotes. Seul l’étude des asymptote est nécessaires.
En ce qui concerne l’étude de la phase, l’argument de G(jw) est donné par :
![]()
Si w tend vers 0, alors l’argument de G(jw) tend vers 0, si w tend vers l’infini l’argument de G(jw) tend vers –p/2. A la fréquence de coupure, pour w égale à w0, l’argument de G(jw) est égal à p/4.

En conclusion, l’étude des diagrammes de Bode permettent de connaître le comportement en fréquence d’un circuit électrique. Seul l’étude en asymptote est nécessaire aussi bien pour le diagramme en amplitude que le diagramme en phase.
Enfin, le dernier intérêt des diagrammes de Bode est que, utilisant des échelles logarithmique, tous les produits se transforment en somme. En conséquence, la majeure partie des diagrammes de Bodes se déduisent des formes de bases par sommation. Ainsi le diagrammes de Bodes du gain complexe :
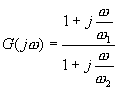
est la somme du diagramme de Bode du gain :
![]()
et du gain :

Les diagrammes de Bodes des formes de base sont regroupés dans le liens suivant :