La numération binaire
![]()
La numération de position est une convention qui permet de coder une valeur exprimée dans une base. Ainsi en base 10 le nombre 2037 s'écrit :
2037(10) = 2.103 + 0.102 + 3.101 + 7.100
Pour écrire ce nombre, les dix symboles arabes : 0, 1, 2, 3, 4 etc. ont été utilisés. Il est possible de coder la même valeur en utilisant d'autre base par exemple la base 2 : le binaire. En base 2, seulement deux symboles peuvent être utilisés : 0, 1. Ainsi le nombre 10101101 en base 2 s'écrit
10101101(2)
= 1.27 + 0.26 + 1.25 + 0.24 + 1.23
+ 1.22 + 0.21 + 1.20
Or sachant que :
| 20 | 1 |
| 21 | 2 |
| 22 | 4 |
| 23 | 8 |
| 24 | 16 |
| 25 | 32 |
| 26 | 64 |
| 27 | 128 |
| 28 | 256 |
| 29 | 512 |
| 210 | 1024 |
le nombre 10101101(2) est égal à 170 (10) puisque :
170 = 128 + 32 + 8 + 4 + 1.
Pour passer la base 10 au binaire, il faut utiliser la méthodes de la division successive par deux. Ainsi par exemple, pour convertir le nombre 54 décimal en binaire, on réalise :
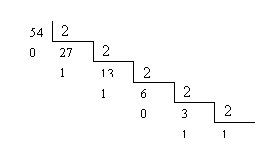
Quelques définitions associées aux nombres binaires :
bit : abréviation de binary unit, il s'agit d'un symbole 0 ou 1.
digit : ensemble de 4bits
octet : ensemble de 8 bits