![]()
La méthode de simplification graphique repose sur les tableaux de Karnaug. Les tableaux de Karnaug regroupe les produits adjacents d'une fonction logique écrit en produit de somme. Il suffit de regrouper les produits où la fonction vaut 1 pour faire apparaître les simplifications. Ainsi pour une fonction à trois variables, le tableau de Karnaug s'écrit :
| b | |||||
| c | |||||
| 00 | 01 | 11 | 10 | ||
| 0 | a.b.c.f(0,0,0) | a.b.c.f(0,0,1) | a.b.c.f(0,1,1) | a.b.c.f(0,1,0) | |
| a | 1 | a.b.c.f(1,0,0) | a.b.c.f(1,0,1) | a.b.c.f(1,1,1) | a.b.c.f(1,1,0) |
Seul les cases où f(a,b,c) est égal à 1 interviennent dans le tableau. Il suffit de regrouper les cases adjacentes par groupe de puissance de deux pour faire apparaître des simplifications.
Ainsi, considérons la table de vérité suivante :
| a | b | c | d | f(a,b,c) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
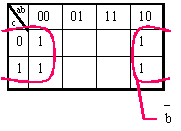
Le tableau de Karnaug correspondant est le suivant :
Considérons maintenant l'exemple suivant :
| a | b | c | f(a,b,c) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
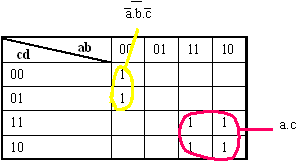
Le tableau de Karnaugh correspondant est le suivant :